Solar Power

(Technology and Economics)

 

The earth receives more energy from the Sun in just one hour than the world's population uses in a whole year.

The total solar energy flux intercepted by the earth on any particular day is 4.2 X 10¹⁸ Watthours or 1.5 X 10²² Joules (or 6.26 X 10²⁰ Joules per hour ). This is equivalent to burning 360 billion tons of oil ( toe ) per day or 15 Billion toe per hour.

In fact the world's total energy consumption of all forms in the year 2000 was only 4.24 X 10²⁰ Joules. In year 2005 it was 10,537 Mtoe (Source BP Statistical Review of World Energy 2006)

Solar Radiation

Sunlight comes in many colours, combining low-energy infrared photons (1.1 eV) with high-energy ultraviolet photons (3.5 eV) and all the visible-light photons between.

The graph below shows the spectrum of the solar energy impinging on a plane, directly facing the sun, outside the Earth's atmosphere at the Earth's mean distance from the Sun. The area under the curve represents the total energy in the spectrum. Known as the "Solar Constant" G₀, it is equal to 1367 Watts per square metre (W/m²).

The radiant energy falling within the visible spectrum is about 43% of the total with about 52% in the infra red region and 5% in the ultra violet region.

The graph below shows the energy at sea level.

Direct energy is the energy received directly from the sun.

Global energy includes energy diffused, scattered or reflected from clouds and energy re-radiated by the earth itself.

Energy received at sea level is about 1kW/m² at noon near the equator

Irradiance and Insolation

Total solar irradiance is defined as the the amount of radiant energy emitted by the Sun over all wavelengths, not just visible light, falling each second on a 1 square metre perpendicular plane outside Earth's atmosphere at a given distance from the Sun. It is roughly constant, fluctuating by only a few parts per thousand from day to day.

On the outer surface of the Earth's atmosphere the irradiance is known as the solar constant and is equal to about 1367 Watts per square meter.

The amount of solar energy that actually passes through the atmosphere and strikes a given area on the Earth over a specific time varies with latitude and with the seasons as well as the weather and is known as the insolation (incident solar radiation).

When he Sun is directly overhead the insolation, that is the incident energy arriving on a surface on the ground perpendicular to the Sun's rays, is typically 1000 Watts per square metre. This is due to the absorption of the Sun's energy by the Earth's atmosphere which dissipates about 25% to 30% of the radiant energy.

Insolation increases with altitude

The terms "irradiance" and "insolation" are often used interchangeably to mean the same thing.

Available Solar Energy

Since the Earth's cross sectional area is 127,400,000 km², the total Sun's power it intercepted by the Earth is 1.740×10¹⁷ Watts but as it rotates, no energy is received during the night and the Sun's energy is distributed across the Earth's entire surface area, most of which is not normal to the Sun's rays for most of the day, so that the average insolation is only one quarter of the solar constant or about 342 Watts per square meter. Taking into account the seasonal and climatic conditions the actual power reaching the ground generally averages less than 200 Watts per square meter. Thus the average power intercepted at any time by the earth's surface is around 127.4 X 10⁶ X 10⁶ X 200 = 25.4 X 10¹⁵ Watts or 25,400 TeraWatts.

Integrating this power over the whole year the total solar energy received by the earth will be:

25,400 TW X 24 X 365 = 222,504,000 TeraWatthours (TWh)

To put this into perspective, the total annual electrical energy (not the total energy) consumed in the world from all sources in 2011 was 22,126 TWh (International Energy Agency (IEA)). Thus the available solar energy is over 10,056 times the world's consumption. The solar energy must of course be converted into electrical energy, but even with a low conversion efficiency of only 10% the available energy will be 22,250,400 TWh or over a thousand times the consumption. Using the same low conversion efficiency, the entire world's electricity demand could be supplied from a solar panel of 127,000 km². Theoretically this could be provided by six solar plants of 21,100 km² or 145,3 km per side, one plant in each of the hot, barren continental deserts in Australia, China, the Middle East, Northern Africa, South America and the USA or one large solar plant covering 1% of the Sahara desert.

Unfortunately the Sun's bounty can only be harvested during daylight hours and some energy must be stored for use during the hours of darkness and the requirement to distribute the energy over great distances to where it is needed make this proposition impractical. The example merely serves to illustrate the abundance of the sun's energy.

What is practical however is to build smaller, more efficient solar power plants to serve the demands of local communities using free solar energy when it is available in conjunction with other other energy sources or some local energy storage where possible. Despite this, less than 0.1% of the world's primary energy demand is supplied by solar energy.

While using photovoltaic solar cells to to supply the world's electrical power needs may be technically practical, is still the most expensive way to generate electricity. See chart of Electricity Generating Costs and Domestic Solar PV System Economics

Equivalent Hours of Full Sun (EHS)

Because of the variation in the intensity of the Sun's radiation during the day and also the variations in the length of the day it is difficult to make comparisons of the Sun's energy falling upon the Earth at different locations. The graph opposite shows an example in which the insolation reaches 1000 W/m2 at noon when the sun is at its highest point in the sky. An insolation of 1000 W/m2 is known as the "Full Sun". Most of the time the incident energy is below this value because it depends on the angle of incidence of the Sun's rays with the ground, increasing during the day from a very low value at dawn as the Sun rises to a peak at noon and falling again as the Sun sets. (See Angle of Incidence below). Similarly the insolation will be reduced as higher latitudes due to the effect of air mass - (See below). The graph also shows that, in this case, the total received energy over the 10 hours of daylight will be 3.5 kWh. If the insolation had been constant at 1000 W/m2 the same amount of energy would have been received in 3.5 hours. The Equivalent Hours of Full Sun is a measure of average insolation at different locations. In this case the EHS is 3.5 hours. The available solar energy and thus the Equivalent Hours of Full Sun (EHS) also depend on the atmospheric conditions of cloud cover and pollution. See Available Energy - Practical Systems below. The concept of EHS is useful for comparing the potential of solar energy systems when installed at different geographic locations.

 

Capturing Solar Energy

Solar energy can be captured in two forms, either as heat or as electrical energy.

• Thermal Systems
Thermal systems capture the Sun's heat energy (infra red radiation) in some form of solar collector and use it to mostly to provide hot water or for space heating, but the heat can also used to generate electricity by heating the working fluid in heat engine which in turn drives a generator.
• Photovoltaic Systems
Photovoltaic systems capture the sun's higher frequency radiation (visible and ultra violet) in an array of semiconductor, photovoltaic cells which convert the radiant energy directly into electricity.

The actual solar energy or insolation reaching a solar collector or array depends on its position on the Earth, its orientation and it also varies continuously with time as well as weather conditions.

The amount of energy captured is directly proportional to the area of the Sun's energy front intercepted by the collector.

Some Geometry

The orientation of the solar collector or the photovoltaic array with respect to the position of the Sun is a major determinant in the efficiency of the solar power system.

• Inclined Planes

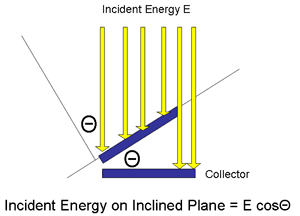
Angle of Incidence The amount of energy impinging on a collector or array is directly proportional to the area of the radiation wave-front it intercepts. For optimum energy capture the collector must be perpendicular to the Sun's rays when the angle of incidence is 90°. For a flat plate on the ground this occurs only when the Sun is directly overhead. Unfortunately unless you live in the tropics this will never be the case and solar arrays must be tilted towards the Sun to receive the maximum insolation. When the incident energy is not perpendicular to the collector, the angle of incidence is (90° - Θ) and the effective area of the collector isA.cosΘ where A is the area of the collector and Θ is the deviation from perpendicular of the radiation.

In the diagram above, the Air Mass corresponds to the factor (1/cosΦ)

Air Mass The Air Mass is a dimensionless quantity defined as the ratio between the actual path length of the solar radiation through the atmosphere and the vertical path length through the atmosphere at sea level. If the Sun's radiation is not perpendicular to the Earth, the transit path through the Earth's atmosphere will be longer and hence the energy absorbed on the way to the collector or array will be greater. The effect of the longer route through the atmosphere is to increase the energy absorption (or lost energy) by a factor of 1/cosΦ where Φ is the deviation from perpendicular of the radiation, also called the zenith angle. Thus in the polar regions as Φ approaches 90 degrees (cosΦ>0) the insolation is very low, even if the collector is pointed directly at the Sun, due to the longer path through the atmosphere.

• Altitude
Insolation increases with altitude since the radiation passes through less air mass hence the energy absorption by the atmosphere is less.

Some Astronomy

To calculate how solar insolation varies with time and with the position of the collector on the Earth's surface we need to know a little astronomy.

Though the Earth moves around the Sun, for the purposes of calculating the energy intercepted by our collectors it is often convenient to assume that the Earth is stationary and the Sun moves relative to the earth in much the same way as the ancients did before Copernicus pointed out their error. Assuming the Earth does not rotate, the apparent trajectory of the Sun follows a two-dimensional plane in the sky called the ecliptic.

• Position
The position of the Sun in the sky relative to an observer on Earth is defined by its altitude angle α (solar elevation angle) and its azimuth angle Ψ.



• The Earth's Orbit
The Earth orbits the Sun with one revolution per year in an elliptical orbit with the Sun at one of the foci of the ellipse. The orbit's two foci are very close together however so that the orbit is almost circular, the distance to the Sun from the perihelion, the point in its orbit closest to the Sun, being only about 3% less than its distance from the aphelion, its furthest distance.


Because the orbit is almost circular, the effect of the orbit on solar irradiance remains essentially constant throughout the year as the Earth orbits the Sun. The actual energy received at any distance from the Sun is determined by the inverse square law. Thus a 3% change in distance gives rise to a 6% change in the irradiance.


• The Earth's Rotation
The Earth's rotation of once per day defines our day and night. As the Earth rotates the insolation at any point on its surface rises to a maximum at mid day and falls to zero during the night as the Earth presents a different face towards the Sun. For maximum efficiency the orientation of the collector should follow the Sun as it passes overhead from East to West.


• Latitude
A solar collector or array placed on the ground will only receive the maximum insolation when the Sun is directly overhead. Because the Earth is roughly spherical, the angle between the plane of the Earth's surface and the incident solar radiation will gradually increase from 90 degrees as we move away from the equator to the upper and lower latitudes by an angle Θ equal to the latitude of the observer. At this point the altitude angle α of the Sun will be (90 - Θ) degrees. Because of the increased inclination of the Earth's surface the insolation received by a collector placed on the surface will gradually decrease.


This drawback can be overcome by inclining the collector so that it is perpendicular to the Sun's rays. The amount of elevation from the horizontal, the tilt angle, should be equal to the latitude angle Θ of the location of the collector.


For maximum effect the axis of the inclination should be perpendicular to the polar axis. That is, in the Northern hemisphere the direction of the collector should point due South.
Note that the polar axis is not the same as the compass bearing because the magnetic poles do not necessarily line up exactly with the geometric poles. The angle between the magnetic and geographical meridians at any place is called the magnetic declination or variation and can be as much as 20 degrees or more. It is expressed in degrees east or west to indicate the direction of magnetic north from true north.


Unfortunately the Sun does not appear to follow a constant path in the Earth's equatorial plane. It appears to move North in the Summer and South in the Winter. In fact the Sun is stationary and the effect is due to the tilt of the Earth's axis of rotation.


• The Earth's Tilt
The Earth's rotational axis is tipped over about 23.45 degrees from the plane of its orbit. This tilt is essentially constant, maintained in that direction due to the gyroscopic action of the earth's rotation, and always points in the same direction relative to the stars, so that the North Pole points towards the star Polaris, the North Star. Over very long time periods however, measured in thousands of years, the direction of Earth's axis slowly changes due to gyroscopic precession.




The fixed orientation in space of the Earth's axis as it orbits the Sun determines the length of the day and creates the world's seasons. At the summer solstice, the longest day,. the northern half of the Earth is pointing towards the Sun creating summer in the Northern hemisphere. The winter solstice, the shortest day in the Northern hemisphere occurs when the Earth has travelled 180 degrees around its orbit and the Northern hemisphere is pointing away from the Sun.
From the Earth it appears that the Earth's rotational axis is rocking backwards and forwards. The apparent tilt of the Earth's axis corresponds to the angular position of the Sun at its highest point in the sky with respect to an observation point on the plane of the equator and is called the solar declination δ (Not to be confused with magnetic variation, also called the declination).
The vernal (spring) and autumnal equinoxes, in March and September when the day and night are the same length, occur when the Earth is mid way between the solstices. Then the plane of the tilt is perpendicular to the direction of the Sun from the Earth so that the insolation is the same on both hemispheres.


As a result of the Earth's tilt, the intensity of the insolation varies during the year giving rise to the seasons. This is not because tilt causes a point on the Earth's surface to move closer to or further from the Sun. The change in distance is negligible. It is because of three factors:
• The Earth's apparent tilt changes the angle of incidence of the solar radiation, changing its insolation per unit area as noted in the diagram above.
• At the same time the tilt also changes the path length of the radiation through the atmosphere which in turn changes the amount of the Sun's energy absorbed by the atmosphere. (also shown in the same diagram above).
• The tilt also changes the number of daylight hours.
These factors all work together to reduce both the intensity and daily duration of the insolation during winter months.


As seen from the northern hemisphere of the Earth, the declination in the elevation of the Sun varies during the course of the year between minus 23.45° in the summer and plus 23.45° in the winter.
Taking into account the solar declination, the altitude angle α of the sun is (90 - Θ ± δ) degrees.
The inclination angle of solar collectors from the horizontal for maximum efficiency should therefore be (Θ ± δ) degrees and the collector should be able to follow this variation in declination throughout the year.


• Time
Fortunately as a source of renewable energy the Sun is much more predictable than the wind. It comes up every morning and goes down every night. The intensity of the wind may be extremely variable, but it is available 24 hours per day, while solar power is only available during daylight hours. At least solar power is reliable and is available when it is needed most - during peak demand hours.


Though the insolation is subject to two temporal variations, a diurnal (daily) cycle due to the Earth's rotation and a yearly cycle due to the tilt of the Earth's axis, we know precisely the magnitude of these effects at any time so we can design our solar power systems accordingly. What is less predictable however is the affect of the weather.


Unless they are connected to the grid, systems which must provide energy on demand need some form of energy storage or an alternative source of energy for the hours of darkness.

Some Meteorology

Unfortunately we have no control over the weather. Overcast skies can severely reduce the energy received on the ground. Obviously solar power generating plants are best located in regions with minimum cloud cover, dust and air pollution. At least we usually have statistics about regional weather conditions to help in choosing suitable locations for solar power plants.

For dimensioning a solar power generating system it is essential to know the number of hours of daylight expected at the site location. This can normally be obtained from national meteorological services and environmental research establishments as well as from NASA in the USA. It helps even more if they are able to provide tables of expected solar energy for the region.

Note: It is important to check the basis of the data. Some organisations quote the solar insolation on a horizontal surface, that is the ground. Others base their data on the insolation of a collector with a fixed angle of tilt corresponding to the latitude of the location.

Energy Capture and Collector / Array Orientation

The table opposite shows how the effectiveness of a solar array or collector diminishes as its orientation and tilt move away from the optimum position. The example shows that to capture maximum solar energy with an array located at a latitude of 35° North, the optimum array orientation is pointing due South and the optimum tilt is the same as the latitude, in this case 35°. If the array system has to be mounted on a roof with a pitch of 45° on a building pointing South West it will only receive a maximum of about 90% of the available solar energy.

Solar Tracking

As indicated above the amount of energy captured by a solar system can be maximised if the collector can follow the ecliptic path of the Sun so that the plane of the collector or array is always perpendicular to the direction of the Sun.

Automatic mechanical tracking systems make it possible to track both the azimuth and the elevation of the Sun's position to maximise energy capture.

Note the lower zenith and the reduced azimuth range of the winter Sun. The chart below shows that, in the UK, the available energy from the winter Sun is between one sixth and one twelfth of the energy from the summer Sun depending on the latitude.

• Azimuth Tracking
Azimuth tracking keeps the collector pointing at the Sun as the Earth rotates.
The insolation varies between zero and its maximum value during the course of every day and remains around its maximum value for a relatively short period of time. Azimuth tracking enables the collector to follow the Sun from East to West throughout the day and brings the most benefits.
Passive systems provide the simplest form of azimuth tracking. They have no motors, controllers or gears and they don't use up any of the energy captured by the collector. They depend on the differential heating of two interconnected tubes of gaseous refrigerants, one on either side of the collector. If the collector is not pointing towards the Sun, one side heats up more than the other and vaporises its refrigerant. The resulting change in weight is used in a mechanical drive mechanism to turn the collector towards the Sun where it will remain when the temperature and weight of the two tubes will be balanced.
Active tracking is also possible by employing temperature sensors and a control system with linear actuating motors taking their drive power from the system.


• Altitude/Elevation Tracking
Elevation tracking enables the collector to follow the seasonal variations in the Sun's altitude but the economic benefits are less than for azimuth tracking.
Compared with the daily variations in insolation, the seasonal variations are very slow and the range of the variation, due to the solar declination is much more restricted. Because of this, reasonable efficiency gains can be obtained simply by manually adjusting the elevation of the collectors every two months. To avoid the cost and complexity of elevation tracking, it may be more cost effective just to specify larger collectors.


• Dual Axis Tracking
Combining azimuth and elevation tracking enables the installation to capture the maximum energy using the smallest possible collectors but the systems are complex and many installations get by with just azimuth tracking.

Solar Collectors

A solar collector is simply a heat collecting surface which intercepts the Sun's radiated energy and heats up a thermal working fluid. In practical thermal systems it is usually more convenient to focus the Suns heat energy on to a small receiver in order to obtain a higher temperature rise of the working fluid. Such collectors are called concentrators. The units used by the solar concentrator community to express the degree of concentration of the mirror system, similar to the magnification factor of a lens are called "Suns". Note that this unit is not a precisely defined quantity.

Concentrators

Typical concentrators are constructed from parabolic mirrors which reflect the Sun's parallel rays on to a single spot at the focus of the mirror.

• Parabolic Dish
A parabolic dish will capture the energy intercepted by the dish and concentrate it on a suitable heat absorber located at the focus. The amount of energy captured and hence the temperature rise of the absorber will be proportional to the area of the dish. Size limitations of the dish limit its application to small systems of from 10kW to 50kW.
• Parabolic Trough
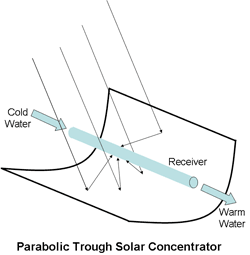
Larger systems use arrays of parabolic trough shaped mirrors oriented north-south to concentrate the solar radiation. They usually also include a tracking system to track the Sun's path throughout the day.

Source: US DOE (EERE)

The thermal absorber, a tube located at along the focal line of the mirror, contains the working fluid which is heated by the solar radiation to a high temperature and used to drive a heat engine.

• Power Tower
An alternative concentrator arrangement is the Power Tower which uses a large array of parabolic mirrors focused on a solar furnace mounted on the top of a tower. Because of the long focal length, the mirrors are almost flat.



As with the trough concentrators, the solar furnace is used to raise steam to drive a turbine generator.


• Heliostats are sun tracking mirrors which are used to reflect the sun onto the top of a solar power tower.

Source David66

This is an example of a heliostat from the THÉMIS experimental station in France. The mirror rotates in both azimuth and elevation.




Source: U.S. NASA

This photograph below shows a solar-thermal power project near Daggett, California. Every mirror in the field of heliostats reflects sunlight continuously onto the receiver on the tower.

Available Energy - Practical Systems

The table below shows the solar energy available at two extremes of latitude and provides an indication of the upper and lower limits of the solar energy falling on the Earth. The insolation (kWh/m²/day) is the monthly averaged incident energy falling on a horizontal surface at the given location. Also called the "Equivalent Sun Hours" or "Hours of Full Sun" (See Definition)

Solar Energy Available at Different Latitudes
Location	Latitude Degrees	Altitude Metres	Tracking	Insolation kWh/m2/Day
				June	December
Anchorage, Alaska	61.17°N	35	None	4.5	0.6
			2 Axis	6.8	0.7
Quito, Equador	0.47°S	2851	None	4.38	4.81
			2 Axis	6.09	6.62

Source NREL

Because of cloud cover and pollution, the quoted hours of "full Sun" are substantially less than the actual hours of daylight. In sunnier climes, an average of 33% of solar irradiation comes from diffuse light but for the majority of locations this is typically more than 50%. The equivalent hours of full Sun takes into account the affect of overcast or partially cloudy skies.

System Dimensioning - Energy Capture

Much care is needed in specifying solar array sizes to meet system power requirements. Using yearly average insolation figures for the chosen location may be acceptable if all that is required is a grid connected system with an average annual generating capacity, but this is almost never the case and it certainly does not apply to stand alone systems.

Averages can be very misleading, even within the month.

The following table gives the monthly average, and yearly average, insolation at two locations in the UK.

Daily Insolation Levels (kWh/m2/day) at Locations in the UK
Location	Latitude	Longitude	Jan	Feb	Mar	Apr	May	June	July	Aug	Sept	Oct	Nov	Dec	Average
Edinburgh	55' 55" N	3" 10" W	0.44	0.94	1.86	3.18	4.33	4.34	4.13	3.41	2.43	1.2	0.59	0.32	2.26
London	51' 32" N	0' 5" W	0.67	1.26	2.22	3.48	4.54	4.51	4.74	4.01	2.86	1.65	0.89	0.52	2.61

Monthly Averaged Insolation Incident On A Horizontal Surface (kWh/m²/day)

Source NASA

If the system capacity were to be based on the yearly average, for most practical installations there would be a surplus of energy in the summer and a shortfall in winter. A stand alone system would have to be dimensioned to be able to provide the peak load during the winter months, otherwise an auxiliary source of power must be provided. The system would then be over-specified for the summer months and some form of reducing the capacity or dumping the excess energy must be found. A hybrid system combining wind and solar power could be the answer.

Electrical Energy Storage

Because no power is provided during the hours of darkness, the stand alone systems must generate and store sufficient energy during the day to satisfy the peak daily load. The storage should also be sufficient to cover several days when no sunlight is available. Batteries are normally used as a buffer to provide the necessary storage to guarantee short term continuity of supply by storing surplus energy during the day for use during the night and during periods of overcast skies. Unfortunately it is not practical to store the summer's surplus energy for use during the winter. See alternaitive Thermal Storage below

Solar Power Generation (Thermal)

Electricity generation in a solar thermal plant occurs in two stages. First the heat energy from the Sun is captured and used to heat a working fluid which is then used in a second energy transformation stage to generate the electricity. Note that the thermal energy comes from the Sun's radiation and not from the air whose temperature will usually be much lower than the temperature of the working fluid. The actual operating temperature reached by the working fluid will depend on the rate at which the thermal energy is being extracted by the working fluid (the flow rate) and delivered to the electricity generating system.

A solar thermal power plant usually has a system of mirrors to concentrate the sunlight on to an absorber, the absorbed energy then being used to power a heat engine which in turn drives a rotary generator. In large scale systems, the heat engine is usually a turbine driven by steam or other vaporous working fluid. In small scale systems the heat engine may be a Stirling engine.

Electricity Generating Systems

Large Scale Solar Thermal Plants

The system below is designed to capture the thermal energy radiated from the sun.

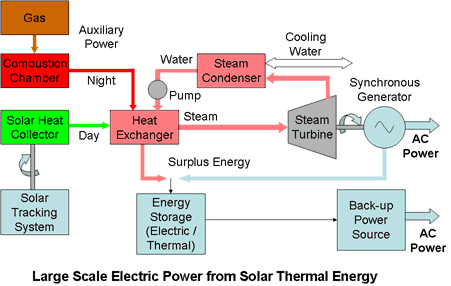
Thermal energy from the Sun is intercepted by a concentrator which focuses the energy on a heat absorber containing the working fluid, usually a synthetic oil, which is heated by the solar radiation to a high temperature typically 400° C. The system may use a binary cycle in which the heated oil is passed through a heat exchanger to raise steam which is used to drive a conventional turbine and generator in a separate circuit.

To maintain the thermal efficiency of the turbine, the working fluid leaving the heat exchanger should not be allowed to cool down. Solar plants are therefore supplemented by gas-fired boilers which generate about a quarter of the overall power output and maintain the temperature overnight.

Several such installations in modules of 80 MW are now operating and solar conversion efficiencies of between 15% and 23% have been achieved. Each module requires about 50 hectares of land and needs very precise engineering and control. Power costs are two to three times that of conventional sources.

Thermal Energy Storage

The use of molten salts to provide the capture, storage and release of solar energy has recently been demonstrated. (See Alternative Storage). The solar thermal energy may be captured directly by a molten salt which has a high thermal capacity in a "Power Tower" or indirectly in a heat exchanger from the hot working fluids circulating through arrays of solar concentrators. A suitable salt such as potassium nitrate is liquid above 370 °C (698 °F) and acts as a second working fluid. It gives up its heat when required to water in a second heat exchanger to form steam for driving the turbine.

The Solana concentrating solar thermal plant in Arizona which uses molten salt storage can keep delivering power for six hours after sunset.

Small Scale Thermal Plants

Steam turbines are only practical for very large installations. Stirling Engines are often used in small systems to drive the electrical generator.

Solar Stirling

Domestic thermal generating plants typically use an array of water filled panels or a small array of parabolic trough concentrators to capture the Sun's thermal energy. Very small system such as those used in space applications may simply use a parabolic dish to capture the energy.

The working fluid is then used as the external heat source for powering the Stirling engine which in turn drives a rotary generator.

An off-grid stand alone solar electric system must have batteries supported by Balance-of-System (BOS) components including chargers, inverters and controllers to manage the energy flows in order to provide power on demand. This makes the system very expensive. Grid connected systems also need power conditioners and control systems if surplus energy is to be sold back to the utility company.

Efficiencies achieved with small scale systems range from 18% to 23%.

Domestic Water Heating Applications - A brief diversion

Many small domestic solar thermal systems are merely used for water heating and not for generating electricity.

• Practical Systems
The working fluid is water, circulating through a rooftop mounted solar panel and fed directly into the domestic hot water system. As an alternative, the working fluid may be passed through a heat exchanger consisting of a coiled pipe in the hot water storage tank to heat the water indirectly.
The front surface of the solar panel is double glazed, allowing the Sun's radiation to pass through to heat up the water flowing through the panel while preventing heat loss from the warmer water due to convection and conduction in the opposite direction (from the panel to the colder atmosphere). The rear surface of the panel is also insulated to prevent heat loss in that direction.
The system works in cold weather because the water is heated by the Sun's radiation, not by the ambient air from which it is insulated.


• Water Temperature
An elegant, self regulating solution for maintaining the water temperature is provided by incorporating a small, subsidiary photovoltaic panel (see below) to generate the electrical energy needed to power the water circulation pumps instead of using mains electricity.
At sunrise, the pump remains switched off until the water reaches its operating temperature at which point the pump is switched on. As the Sun's radiation increases during the morning, the water temperature will rise, but at the same time the solar powered pump will run faster, increasing the water flow and thus transfering heat more quickly from the panel to the hot water storage tank. By suitably dimensioning the pump and the photovoltaic panel, the heat transfer rate from the panel can be matched to the heat absorption rate from the Sun thus maintaining a constant water temperature. As the received Sun's energy wanes in the afternoon the process is reversed, the pump runs more slowly reducing the rate at which heat is extracted from the panel thus maintaining its temperature. Being completely independent of the electricity grid, these systems have the added economic and environmental benefits that no electrical energy is drawn from the grid for running the pumps.
• Temperature Limits
With water as the working fluid, the system is prone to freezing and boiling unless special precautions are taken. Low cost systems allow the water to freeze in very cold and dark environments by using flexible freeze-tolerant, silicone rubber pipework which is sufficient to accommodate the expansion of the water as it turns to ice. The volume of water used in solar thermal panels is very small, typically around 2 or 3 litres and is spread over a very large area to capture the maximum solar radiation. The high received radiation acting on a low water volume enables the water to heat up very quickly but for the same reason makes it susceptible to boiling. Unless there is a constant water flow to a storage tank with the heated water in the panel being replaced by cold water from the tank, the water could reach temperatures of 150 degrees C or more and for this reason the water pumps must be continually switched on. Even so, the possibility of boiling still remains, even with the pumps running, if the system is incorrectly dimensioned. The equilibrium temperature reached will depend on the balance between the solar energy captured by the panel and the thermal energy absorbed in the storage tank, the rate at which it is withdrawn from the tank and the system heat losses. Using a very small panel coupled to a very large tank with high hot water usage will result in a low water temperature in the tank. Conversely using a very large panel with a very small tank could result in boiling, particulaly if the hot water usage is very low. This need not be a disaster since the water content in the panel is very low and system could be designed to allow the steam to vent in case of boiling.
• Efficiency
Energy conversion efficiencies achieved in these pure thermal applications may be three or four times the efficiency of photovoltaic applications though their applications are much more limited.
• Economics
In higher latitudes the available solar energy captured by practical domestic installations may be sufficient to provide hot water for washing and showering but not enough to supply building space heating requirements during the colder months. Back-up heating systems will consequently be needed to cater for the base load to satisfy these requirements. Because the supply of solar energy is intermittent, the conventional heating system must fill in the gaps and there is little opportunity to downsize it. The householder will therefore, most likely have to pay the capital costs of a base load system capable of supplying the full heating load as well as the solar heating system even though the conventional heating system will not be working at full capacity most of the time.
Domestic solar thermal systems may not generate electricity directly but they do contribute to a reduction in the use of electrical energy and its associated costs.
• Example
Useful Energy Captured
The table above shows that in the UK, the average solar radiation received is about 2.5 kWh / M² / day. A single solar panel with an area of 3 M² will therefore capture 2.5 x 3 x 365 = 2737 kWh of energy per year. With a system conversion efficiency of around 40% and less than optimal orientation of a typical rooftop mounted solar panel, the maximum usable energy received by a single panel system will be around 1000 kWh. This is roughly equivalent to the energy supplied by a 3 kW immersion heater used for one hour per day. As always however, averages can be misleading. In the summer, the solar panel could deliver an"average" of about 5 kWh of heating energy per day, but in the winter this could be as low as 0.4 kWh per day. The energy captured can of course always be increased by increasing the number of solar panels employed in the system.
Cost Savings
The cost saving will depend on whether the solar system is replacing 1000 kWh of heating energy supplied by a gas or an electric water heating system and the associated tarriff charged for the energy. With UK domestic gas currently costing less than £0.03 per kWh ($0. 045) and electricity costing about £0.10 per kWh ($0.15) the annual savings are likely to be somehwere between £30 and £100 ($50 to $150).
Since typical single panel installations cost around £2,500 or £3,000 ($4,000 to $5,000), unless the systems qualify for a government subsidy or there is a very large increase in energy costs, the payback time for the investment will be measured in decades rather than years. Saving the planet can be quite expensive.
Carbon Footprints
As with wind power, if the investment fails the conventional economic tests, the notion of carbon footprints is often used to jusify the expense, based on the potential for reducing the amount of greenhouse gases emitted by alternative methods of power generation.


See also Domestic Solar PV System Economics below.

Solar Power Generation (Voltaic)

Solar voltaic power generation is the direct conversion of solar energy into electricity.

Sunlight comes in many colours, combining low-energy (1.1 electronVolts (eV)) infrared photons with high-energy (3.5 eV) ultraviolet photons and all the rainbow of visible-light photons in between. Solar cells, also called photovoltaic or PV cells, are semiconductor devices designed to capture these photons and convert their energy directly into electrical energy.

How Solar Cells Work

When a photon with sufficient energy impinges upon a semiconductor it can transfer enough energy to a electron to free it from the bonds of the semiconductor's valence band so that it is free to move and thus carry an electric current. The junction in a semiconductor diode provides the necessary electric field to cause the current to flow in an external circuit.

A more detailed explanation of how solar cells work is given in the section on photovoltaic diodes.

Conversion Efficiencies

The typical output voltage of a PV cell is between 0.5 and 0.6 Volts and the energy conversion efficiency ranges from less than 10% to over 20%. An array of cells can therefore generate about 200 Watts of electrical power per square metre when illuminated by solar radiation of 1000 Watts per square metre. The corresponding current density will be about 400 Amps/m². Because of climatic conditions the intensity of the insolation rarely reaches 1000 W/m².

Practical cells are also much smaller than one square meter with actual sizes of commercially available cells ranging from about one centimetre square to 15 centimetres square. The corresponding output Wattages for these cells range from 20 milliWatts to about 4 Watts.

Solar PV systems are amongst the least efficient ways of generating electricity, (see Efficiency Comparison Table), but this poor performance is not just due to the low PV conversion efficiency of the cells which is improved year by year by ongoing research and development. It is mainly due to the lack of available sunshine, and no amount of R&D can improve that.

A PV conversion effifiency of 15% may appear to be very low, but it is on a par with the "well to wheel" conversion efficiency of the energy used to power a gasoline/petrol driven automobile.

PV Cell and Module Ratings

• Standard Test Conditions (STC)
In order to compare solar cells on a like for like basis a set of Standard Test Conditions (STC) has been defined.
The conditions are: Normal Irradiance of 1000 W/m², Cell Temperature 25 °C (77 °F) and Air Mass =1.5
• Air Mass
The receiving surface corresponding to AM 1.5 is defined as an inclined plane at 37° tilt (the average latitude in the USA) toward the equator, facing the sun. In this case, the surface normal points to the sun, at an elevation of 48.81°, its zenith angle, above the horizon.
• Rated Power
Rated Power is defined as the maximum power (Wp or kWp) generated by the cell or module under the Standard Test Conditions.

Alternative PV Cell Rating

The STC laboratory test conditions are not truly representative of typical open air operating conditions and for this reason a more realistic set of test conditions, NOCT, was developed.

• Normal Operating Cell Temperature (NOCT)
Normal Irradiance 800 W/m², Air Temperature 20°C (68°F), Wind Velocity (cooling) of 1 meter per second (2.24 miles per hour), with the rear side of the solar panel open to the air flow.
• Air Mass and Rated Power similar to STC

Interpretation and Application of the STC and NOCT Ratings.

The following is an example of key data taken from a reputable manufacturer's specification sheet for a 250 Watt solar panel.

• Information provided:

  STC rating 250 Wp
  NOCT raring 183.3 Wp
  Cell dimensions 156 mm X 156 mm
  Number of cells 60

No mention of the area
No mention of conversion efficiency
• What does this mean in practice
• The STC and NOCT ratings are the power outputs achieved under test conditions.
• The test conditions are designed to represent the maximum solar energy which could be received under ideal conditions.
• In practice you will never achieve these power outputs from sunlight
• The STC and NOCT ratings assume a constant high level of irradiance (1000 W/m²or 800 W/m²). These are simply different standard input power levels used for the tests, thus any cell will normally generate a larger output power under STC conditions compared with NOTC conditions.
• Outside of the tropics, the irradiance from the Sun at ground level on typical solar panels will rarely even approach these test levels.
• The insolation which is the average effect of the Sun's irradiance, taking into account, the hourly, daily, and seasonal variations as well as latitude and local climate conditions, will be much lower than the test irradiance. The NREL maps on the Going Solar page indicate the expected regional insolation levels.The consequence is that the average solar energy intercepted by the panels will be very small and the corresponding electrical energy output from the panels will also be very small.
• The actual solar energy captured also depends on the configuration of the solar panels and whether they are able to track the Sun during its path across the sky.
•  What will be the average electrical power output from the above "250 Watt" solar panel?
It depends on the location and the type of solar array and the conversion efficiency of the solar PV cells. Assuming a fixed solar array located in the North East of the USA, facing South and tilted towards the Sun at an angle corresponding to the latitude of the site, the NREL map shows that the insolation is around 4 kWh/m²/day. In the sunnier South West the insolation will be about 50% more at 6 kWh/m²/day which translates directly into 50% more electrical output power from the same solar panels.


The 60 cell solar panel has an effective area of 60 X 0.156m² = 1.46 m²
In the North East this panel will therefore intercept 1.46 X 4 = 5.84 kWh of solar energy per day.
This insolation is equivalent to a constant (average) solar power of 5840 / 24 = 243.3 Watts during the 24 hour day.
The conversion efficiency of the solar cells is calculated from the manufacturer's specified electrical power output achieved from the NOCT specified power input.
The energy intercepted by the 1.46 m² panel under NOCT conditions will be 1.46 X 800 = 1168 Watts
The specified electrical output power from the panel is 183.3 Watts
Thus the conversion efficiency = 183.3 / 1168 X100 = 15.7%
Applying this conversion efficiency to the actual insolation of 243.3 Watts gives an average electrical power output from the panel of 243.3 X 0.157 = 38.2 Watts (This corresponds to an electrical output of 26.2 W / m²)


Not bad for a solar panel rated at 250 Watts?!

 

Solar Cell Operating Characteristics

The graph below shows that with constant irradiance the output voltage of a cell or an array of cells falls as it is called upon to deliver more current.

Maximum power delivery occurs the voltage has dropped to about 80% of open circuit voltage voltage.

The Fill Factor (FF) is defined as the ratio between the power at the maximum power point and the product of the open circuit voltage and short circuit current. It is typically better than 75% for good quality solar cells.

The short circuit (SC) current is directly related to the number of photons absorbed by the semiconducting material and is thus proportional to light intensity. The conversion efficiency is therefore reasonably constant so that the power output is proportional to the irradiance down to fairly low levels, however the efficiency is reduced if the cell temperature is allowed to rise. The open circuit (OC) voltage varies only slightly with light intensity.

As temperature increases, the band gap of the intrinsic semiconductor shrinks, and the open circuit voltage (Voc) decreases. At the same time, the lower band gap allows more incident energy to be absorbed because a greater percentage of the incident light has enough energy to raise charge carriers from the valence band to the conduction band. A larger photocurrent results. As the temperature is raised however, the internal resistance of the material increases and the electrical conductivity decreases. The increase in the current for a given temperature rise is thus proportionately lower than the decrease in voltage. Hence the efficiency of the cell is reduced.

Solar Cell Efficiency

The following graphs show the same information as those above but in a slightly different form showing how increased temperature reduces the efficiency.

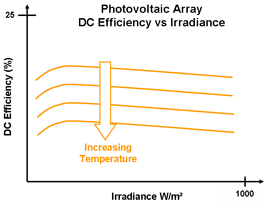
Typically, PV cell power output reduces by about 0.5% with every degree Celsius increase in temperature.

In real outdoor conditions the rated peak power Wp is seldom achieved, since module temperature usually is more in the range of 40°C - 60°C. Efficiency can be improved by cooling the cells and some systems have been designed to make use of the heat absorbed by the cooling fluid in solar heating applications.

NOTE: A hot sunny day is a double-edged sword for a PV cell. Even though the conversion efficiency goes down as the cell heats up, the overall power collected may go up due to the increase in sunlight on the cell.

Solar Cell Types

Several types of solar cells have been developed with the aims of reducing costs and improving efficiencies.

• Crystalline Silicon Solar Cells
Benefiting from the manufacturing experience of the semiconductor industry, crystalline silicon is the leading solar cell material, though still relatively expensive. Monocrystalline cells are cut from single crystals of high purity electronics grade silicon. These cells are about 25 percent efficient at best. Using the easier to manufacture polycrystalline silicon cut from from a block of crystals or less pure, so called "solar grade" silicon, efficiencies may be only about 15% or 16% due to the effect of grain boundaries or impurities but they cost a fraction of single crystal electronics grade cells.
• Amorphous Silicon Solar Cells
Amorphous Silicon has been employed for many years in the manufacture the solar cells used for powering electronic calculators and watches and promises the possibility of low cost, higher power cells. Amorphous material appears like a solid but has no regular crystal lattice structure. Glass is an example of such materials. The presence of controlled quantities of certain "impurity" elements such as hydrogen and the random crystal lattice formation actually enhance the otherwise very low conversion efficiency. Typical cell efficiencies range from 5% to 10%.
Manufacturing yield is still a problem and the cells suffer from degradation when exposed to the sun.
• Thin Film Silicon Solar Cells
Thin film cells are made by depositing the active photovoltaic material, such as amorphous silicon or other semiconductor onto a glass or other substrate together with the necessary current collecting contacts. The cell construction is much less costly than using semiconductor wafers and the manufacturing process is also simpler as well as being suitable for making cells with a much larger area and hence current carrying capability. Efficiencies of 11% to 14% have been achieved with this construction.
PV systems on flexible polymer substrates have also been made using Copper Indium Gallium Selenide (CIGS) active material with efficiencies of 10%.
• Organic PV Solar Cells
Intensive research is being carried out by various teams on the use of organic semiconductors in the construction of PV cells. Devices can be fabricated by means of a printing process from single or double layer organic polymer films sandwiched between a pair of electrodes. Manufacturing does not involve the high energy consumption associated with crystalline semi conductors and brings the possibility of high volume, low cost products printed onto flexible films. Currently, conversion efficiencies are rather low at around 12% but this is expected to improve.
• Multi Layer (Tandem) Solar Cells
Better conversion efficiencies are possible by using multiple layers of differing semiconductor materials, optimised for different wavelengths, in a single device. This can raise the theoretical efficiency limit, currently about 30% for a single junction device, to about 45% for a three junction cell.
Efficiencies of over 33% have already been achieved in practical devices.
• Exotic Materials
Materials such as Gallium Arsenide, Copper Indium Diselenide, Cadmium Telluride and Indium Nitride have been employed to provide particular characteristics to optimise solar cells for specific applications.
Gallium Arsenide is used for military and aerospace applications in a variety of cells in combination with other elements because of it's suitability for capturing high energy photons (ultra violet radiation), high potential conversion efficiency and its ability to withstand high temperatures. It is however more difficult to manufacture and cells using Gallium Arsenide can be 100 times more expensive than commercial silicon based cells.
Copper Indium Diselenide and Cadmium Telluride are used in polycrystalline form in low cost thin film cells because of their ease of manufacture and reasonable yields. Efficiencies are however low ranging from 8% to 14%
Indium Nitride is suitable for capturing low energy photons (infra red radiation) making it suitable for full spectrum devices when used in tandem solar cells in combination with other materials such as Gallium Arsenide which capture the high energy photons.
• Electrochemical Solar Cells - Dye Sensitised Solar Cells (DSSC or Grätzel Cells)
Relatively new, these cells are low cost devices which use dye sensitised Titanium dioxide in combination with a liquid electrolyte to generate the current. Up to now they are only available in small sizes with efficiencies between 7% and 10%.

Solar PV Collectors

Solar cells are usually sold in modules built up from a number of cells arranged in series and / or parallel to provide convenient or commonly used voltages and power ratings.

Solar Arrays

Modules can be similarly interconnected to create larger arrays with the desired peak DC voltage and current.

Concentrators

As with thermal collectors, concentration of the incident energy on to a smaller surface is possible. For very small applications, optical mirrors and lenses are used.

Maximum Power Point Tracking (MPPT)

A power source will deliver its maximum power to a load when the load has the same impedance as the internal impedance of the power source. (Jacobi's Law). Unfortunately, batteries are far from the ideal load for a solar array and the mismatch results in major efficiency losses.

A typical PV array designed to charge 12 Volt batteries delivers its maximum power at an operating voltage around 17 Volts. Lead Acid batteries are normally charged up to 14 Volts though the voltage quickly drops to 12 Volts as they start to deliver current and lower still as the depth of discharge (DOD) increases.
In its simplest form, charging is carried out by connecting the PV array directly across the battery. The battery however is a power source itself and presents an opposing voltage to the PV array. This pulls the operating voltage of the array down to the voltage of the discharged battery and this is far from the optimum operating point of the array.

The diagram below shows the performance of a17 Volt, 4.4 Amp, 75 Watt PV array used to top up a 12 Volt battery. If the actual battery voltage is 12 Volts, the resulting current will only be about 2.5 Amps and the power delivered by the array will be just over 50 Watts rather than the specified 75 Watts: an efficiency loss of over 30%.
Maximum Power Point Tracking is designed to overcome this problem.

The power tracker module is a form of voltage regulator which is placed between the PV array and the battery. It presents an ideal load to the PV array allowing it to operate at its optimum voltage, in this case 17 Volts, delivering its full 75 Watts regardless of the battery voltage. A variable DC/DC converter in the module automatically adjusts the DC output from the module to match the battery voltage of 12 Volts.
As the voltage is stepped down in the DC/DC converter, the current will be stepped up in the same ratio. Thus the charging current will be 17/12 X 4.4 = 6.2 Amps and, assuming no losses in the module, the power delivered to the battery will be 12 X 6.23 = the full 75 Watts generated by the PV array.
In practice the converter losses could be as high as 10%. Nevertheless a substantial efficiency improvement is possible.

It is not enough however to match the voltage at the specified maximum power point (MPP) of the PV array to the varying battery voltage as the battery charges up. Due to changes in the intensity of the radiation falling on the array during the day as well as to changes in the ambient temperature, the operating characteristic of the PV array is constantly changing and with it the MPP of the PV also changes. Thus we have a moving reference point and a moving target. For optimum power transfer, the system needs to track the MPP as the solar intensity and ambient temperature changes in order to provide a dynamic reference point to the voltage regulator.

High performance MPPT modules may incorporate software algorithms to take account of the variations in insolation and temperature. A typical job for fuzzy logic or a neural network. Alternatively the optimisation can be accomplished in hardware by means of a perturbation signal incorporated in a feedback loop which drives the system operating point to the MPP.

A small dither voltage is superimposed on the PV voltage and its affect on the regulator output current feeding the battery is monitored. If the current drawn by the battery increases when the dither voltage increases, then the operating point has moved towards the MPP and therefore, the operating voltage must be increased in the same direction. On the other hand, if the current into the battery decreases, then the operating point has moved away from the MPP and the the operating voltage must be decreased to bring it back.

 

Large Scale Photovoltaic Plants

Several large scale grid connected PV power plants have been constructed throughout the world, mostly of 300 kW to 500 kW capacity but some as high as 300MW or more. Up to now deployment of large scale plants has been limited to experimental installations because of the high cost of the solar panels. With typical efficiencies of around 15%, a 500 kW plant will need around 20,000 square metres of PV panels costing about $1.00 per Watt as well as large scale inverters capable of handling the full system power output. See an example of a Grid Scale Solar PV System.

Small Scale Photovoltaic Plants and Domestic Applications

The diagram below shows the basic building blocks of a small stand-alone off-grid PV power generating system. A grid connected system would not need the battery and MPPT power tracking system. They do however need alternative capacity to come on stream to carry the load during the hours of darkness.

Photovoltaic System Dimensioning

• Array sizes for Photovoltaic System
The following example show the array sizes necessary to generate 10 kWh of usable energy with an average daily insolation of 2 kWh/m²/day. Note that the results are heavily dependent on the efficiency assumptions used.
Needless to say the array must not be shaded by objects such as trees or buildings.


• Example
Energy received per unit area = Insolation X Solar conversion efficiency.
Thus:
The area required for a given energy capture = Energy required ÷ ( Insolation at the desired location X Solar conversion efficiency)
Using an efficient (expensive) photovoltaic array with a conversion efficiency of 15% the area of the array will be:
10÷(2 X 0.15) = 33.3 m²
Insolation data is usually provided for the energy falling on a flat surface. By tilting the array to an angle corresponding to the latitude of the location, an extra 10% of energy can be captured reducing the area required to 30 m². See the diagram showing Array Orientation
This advantage will be lost however if the array is to be mounted on a roof which is not optimally aligned towards the Sun.
If the array is free standing on the ground, and not constrained to be used on a roof, a solar tracking system can be used to enable more of the Sun's energy to be captured. A 30% improvement is possible reducing the required array area to about 21 m²


Note that the PV array output is DC electrical power.
To provide AC power there would be further electrical losses of 10% to 20% in the voltage regulator, inverter and control circuits.


• Grid-connected Systems
Assuming 20 % electrical system losses, a fixed PV array with an area of around 36 m², or a solar tracking PV array of 25 m² would be required to provide 10 kWh of AC power per day.


• Stand Alone Systems
Off-grid systems are subject to the same performance parameters as grid-connected systems however since they also use battery storage they suffer from an extra efficiency loss of up to 30% due to the back emf of the battery.
Unless an MPPT tracking system is used to reduce these losses the array would have to be 30% bigger to compensate. Thus to provide the same 10 kWh of AC power per day in a stand-alone system, the required PV array area would have to be 47 m² for a fixed installation and 33 m² for a solar tracking system.


Electricity consumption in many households in Europe and the USA is 2 or 3 times more than 10 kWh per day, particularly for those willing to invest in solar PV electricity generation. (See Energy Demand Table). This implies that very large PV arrays with areas up to 150 m² or more, probably larger than the available South facing roof surface, would be needed to satisfy their energy demands.


All of the above is based on an average insolation of 2 kWh/m²/day, but in northern temperate zones the winter insolation is likely to be less than a quarter of the average for the location. See the table for Energy Availability and Energy Capture above. Thus the available energy will be only 2.5 kWh/day during the winter months or the systems would need to be four times bigger in order to supply the same 10 kWh/day of electrical energy in the winter.


Domestic Solar PV System Economics
Example
• Costs
According to the UK Government Energy Saving Trust, the costs for installing a solar PV system vary greatly. An average domestic system is quite small generating around 2.2 kWp and costs around £12,000 ($18,000). Larger solar electricity systems can cost in the region of £4,500 ($7,000) to £8,000 ($12,000) per kWp, reducing slightly as the system size increases.
• Benefits
A 2.2 kWp system only delivers the full 2.2 kW of power under Standard Test Conditions of 1000 W/m² insolation. It would generate 52.8 kWH (52.8 Units) of electricity per day if the Sun was directly overhead and shining constantly day and night. But the table above shows that the average insolation in the UK is only about 2.5 kWh/m²/day. This is equivalent to 2.5 hours of full Sun (see EHS above) per day, not 24 hours. Thus the actual electrical energy output from the PV system in the UK will be about 5.5 kWh per day or 2,000 kWh per year.
• Payback
Buying 2,000 kWh of electrical energy from the local utility company would cost £200 ($300) with the curent costs of electricity at £0.10 ($0.15) per unit. Ignoring maintenance costs, this gives a payback period of sixty years.
Fortunately, many governments provide generous grants to subsidise the installation and/or operation of solar power systems thus reducing the capital outlay and decreasing the investment payback time.
•  Selling surplus energy back to the utility company
The average UK household consumes about 5,000 kWh of electrical energy per year or around 14 units per day. The likelihood of a domestic installation as described above having regular surpluses is quite remote.
Furthermore, feeding electrical energy back into the grid involves the obligatory installation of additional, costly metering and safety systems as well as synchronisation electronics so that this option is only economically justifiable for installations with relatively large surplusses.


Beware when the solar panel salesman comes knocking!


See also economics and practicality of Grid Scale Solar PV Systems


See also Domestic Solar Heating and a comparison of Electricity Generating Costs for different fuels.


• Balance of System (BOS) Components
The associated BOS components needed to complete the system are described in the section on Small Scale Systems.

• Other PV System Considerations
Converting the direct current output of the PV array to alternating current is both costly and inefficient. Some of this cost and waste can be avoided by using household appliances designed to run on DC power where they are available.
Similarly it is not sensible to run heaters from PV systems.

Solar energy may be free, but converting it into electrical energy is not.

See also Electromagnetic Radiation

See also Generators

Return to Electrical Energy Supply Overview